12. Monte Carlo Simulation and Linear Algebra¶
12.1. Monte Carlo simulation¶
What is Monte Carlo simulation?
The name Monte Carlo refers to the Monte Carlo Casino in Monaco where Ulam’s uncle would borrow money from relatives to gamble.
It would be nice to simulate the casino, so Ulam’s uncle did not need to borrow money to go.
Actually…,
Monte Carlo is the code name of the secret project for creating the hydrogen bomb.
Ulam worked with John von Neumann to program the first electronic computer ENIAC to simulate a computational model of a thermonuclear reaction.
(See also The Beginning of the Monte Carlo Method for a more detailed account.)
How to compute the value of \(\pi\)?
An application of Monte Carlo simulation is in approximating \(\pi\) using
the Buffon’s needle.
There is a program written in javascript to do this.
The javascript program a bit long to digest, so we will use an alternative simulation that is easier to understand/program.
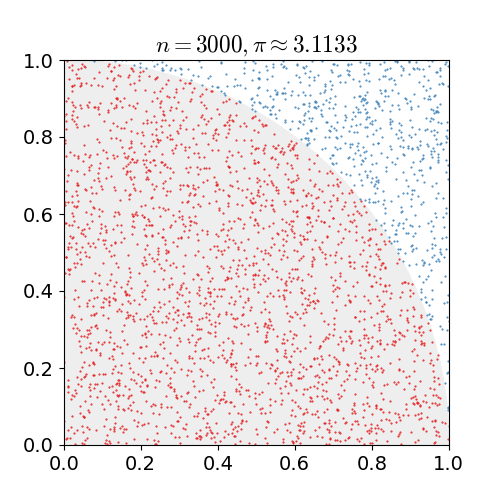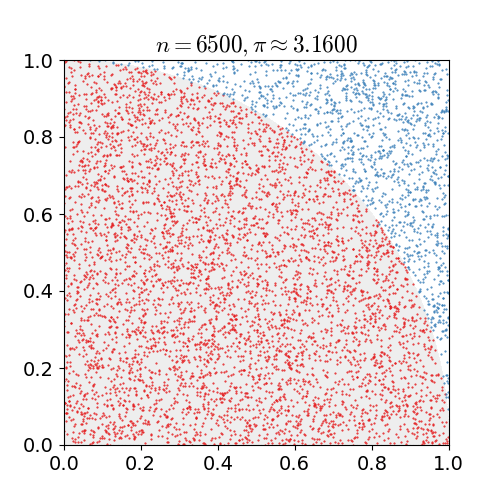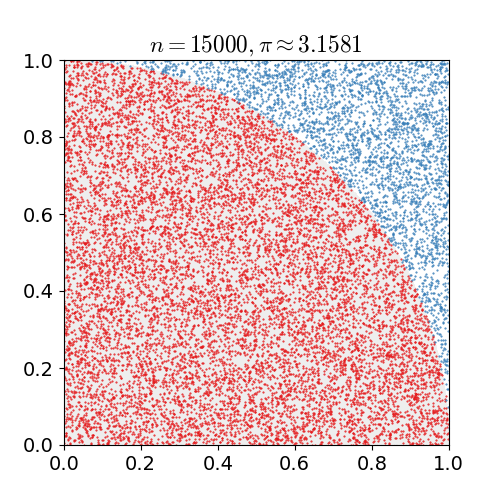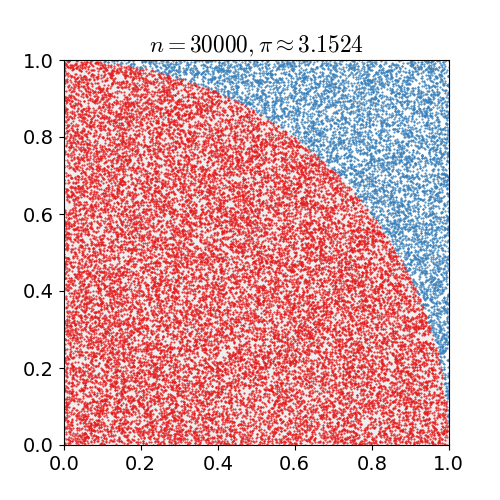
If we uniformly randomly pick a point in a square. What is the chance it is in the inscribed circle, i.e., the biggest circle inside the square?
The chance is the area of the circle divided by the area of the square. Suppose the square has length \(\ell\), then the chance is
independent of the length \(\ell\).
Exercise Complete the following function to return an approximation of \(\pi\) as follows:
Simulate the random process of picking a point from a square repeatedly
ntimes by
generating the \(x\) and \(y\) coordinates uniformly randomly from a unit interval \([0,1)\).Compute the fraction of times the point is in the first quadrant of the inscribed circle as shown in the figure below.
Return \(4\) times the fraction as the approximation.
import random, math
def approximate_pi(n):
### BEGIN SOLUTION
return 4*len([True for i in range(n)
if random.random()**2 + random.random()**2 < 1])/n
### END SOLUTION
print(f'Approximate: {approximate_pi(int(1e7))}\nGround truth: {math.pi}')
Approximate: 3.141502
Ground truth: 3.141592653589793
How accurate is the approximation?
The following uses a powerful library numpy for computing to return a \(95\%\)-confidence interval.
import numpy as np
def np_approximate_pi(n):
in_circle = (np.random.random((n,2))**2).sum(axis=-1) < 1
mean = 4 * in_circle.mean()
std = 4 * in_circle.std() / n**0.5
return np.array([mean - 2*std, mean + 2*std])
interval = np_approximate_pi(int(1e7))
print(f'''95%-confidence interval: {interval}
Estimate: {interval.mean():.4f} ± {(interval[1]-interval[0])/2:.4f}
Ground truth: {math.pi}''')
95%-confidence interval: [3.1408107 3.1428877]
Estimate: 3.1418 ± 0.0010
Ground truth: 3.141592653589793
Note that the computation done using numpy is over \(5\) times faster despite the additional computation of the standard deviation.
There are faster methods to approximate \(\pi\) such as the Chudnovsky_algorithm, but Monte-Carlo method is still useful in more complicated situations.
E.g., see the Monte Carlo simulation of a real-life situation in playing basketball:
“When down by three and left with only 30 seconds is it better to attempt a hard 3-point shot or an easy 2-point shot and get another possession?” –LeBron James
12.2. Linear Algebra¶
How to solve a linear equation?
Given the following linear equation in variable \(x\) with real-valued coefficient \(a\) and \(b\),
what is the value of \(x\) that satisfies the equation?
Exercise Complete the following function to return either the unique solution of \(x\) or None if a unique solution does not exist.
def solve_linear_equation(a,b):
### BEGIN SOLUTION
return b/a if a != 0 else None
### END SOLUTION
import ipywidgets as widgets
@widgets.interact(a=(0,5,1),b=(0,5,1))
def linear_equation_solver(a=2, b=3):
print(f'''linear equation: {a}x = {b}
solution: x = {solve_linear_equation(a,b)}''')
How to solve multiple linear equations?
In the general case, we have a system of \(m\) linear equations and \(n\) variables:
where
\(x_j\) for \(j\in \{0,\dots,n-1\}\) are the variables, and
\(a_{ij}\) and \(b_j\) for \(i\in \{0,\dots,m-1\}\) and \(j\in \{0,\dots,n-1\}\) are the coefficients.
A fundamental problem in linear algebra is to compute the unique solution to the system if it exists.
We will consider the simpler 2-by-2 system with 2 variables and 2 equations:
To get an idea of the solution, suppose
The system of equations become
which gives the solution directly.
What about \(a_{00}=a_{11}=2\) instead?
To obtain the solution, we simply divide both equations by 2:
What if \(a_{01}=2\) instead?
The second equation gives the solution of \(x_1\), and we can use the solution in the first equation to solve for \(x_0\). More precisely:
Subtract the second equation from the first one:
Divide both equation by 2:
The above operations are called row operations in linear algebra: each row is an equation.
A system of linear equations can be solved by the linear operations of
multiplying an equation by a constant, and
subtracting one equation from another.
How to write a program to solve a general 2-by-2 system? We will use the numpy library.
12.2.1. Creating numpy arrays¶
How to store the coefficients?
In linear algebra, a system of equations such as
is written concisely in matrix form as \( \mathbf{A} \mathbf{x} = \mathbf{b} \):
where \( \mathbf{A} \mathbf{x}\) is the matrix multiplication
We say that \(\mathbf{A}\) is a matrix and its dimension/shape is \(2\)-by-\(2\):
The first dimension/axis has size \(2\). We also say that the matrix has \(2\) rows.
The second dimension/axis has size \(2\). We also say that the matrix has \(2\) columns. \(\mathbf{x}\) and \(\mathbf{b}\) are called column vectors, which are matrices with one column.
Consider the example $\( \begin{aligned} 2x_0 + 2x_1 &= 1\\ \hphantom{2x_0 +} 2x_1 &= 1, \end{aligned}\)\( or in matrix form with \)\( \begin{aligned} \mathbf{A}&=\begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix} = \begin{bmatrix} 2 & 2 \\ 0 & 2 \end{bmatrix}\\ \mathbf{b}&=\begin{bmatrix} b_0\\ b_1 \end{bmatrix} = \begin{bmatrix} 1\\ 1 \end{bmatrix}\end{aligned}\)$
Instead of using list to store the matrix, we will use a numpy array.
A = np.array([[2.,2],[0,2]])
b = np.array([1.,1])
A, b
(array([[2., 2.],
[0., 2.]]),
array([1., 1.]))
Compared to list, numpy array is often more efficient and has more useful attributes.
array_attributes = set(attr for attr in dir(np.array([])) if attr[0]!='_')
list_attributes = set(attr for attr in dir(list) if attr[0]!='_')
print('\nCommon attributes:\n',*(array_attributes & list_attributes))
print('\nArray-specific attributes:\n', *(array_attributes - list_attributes))
print('\nList-specific attributes:\n',*(list_attributes - array_attributes))
Common attributes:
sort copy
Array-specific attributes:
dump T argmin repeat itemsize diagonal prod choose compress setfield ndim ptp argmax swapaxes squeeze conj all item trace tofile partition fill mean byteswap getfield max conjugate clip imag ctypes cumprod size data astype reshape dtype std nbytes ravel round resize var setflags newbyteorder argsort dot flatten sum tostring put flags real cumsum flat transpose base dumps tobytes searchsorted strides tolist view min itemset shape any argpartition take nonzero
List-specific attributes:
remove insert append pop reverse clear extend index count
The following attributes give the dimension/shape, number of dimensions, size, and datatype.
for array in A, b:
print(f'''{array}
shape: {array.shape}
ndim: {array.ndim}
size: {array.size}
dtype: {array.dtype}
''')
[[2. 2.]
[0. 2.]]
shape: (2, 2)
ndim: 2
size: 4
dtype: float64
[1. 1.]
shape: (2,)
ndim: 1
size: 2
dtype: float64
Note that the function len only returns the size of the first dimension:
assert A.shape[0] == len(A)
len(A)
2
Unlike list, every numpy array has a data type. For efficient computation/storage, numpy implements different data types with different storage sizes:
integer:
int8,int16,int32,int64,uint8, …float:
float16,float32,float64, …complex:
complex64,complex128, …boolean:
bool8Unicode:
stringObject:
object
E.g., int64 is the 64-bit integer. Unlike int, int64 has a range.
np.int64?
print(f'range: {np.int64(-2**63)} to {np.int64(2**63-1)}')
np.int64(2**63) # overflow error
range: -9223372036854775808 to 9223372036854775807
---------------------------------------------------------------------------
OverflowError Traceback (most recent call last)
<ipython-input-9-b5ecbde7f9e9> in <module>
1 get_ipython().run_line_magic('pinfo', 'np.int64')
2 print(f'range: {np.int64(-2**63)} to {np.int64(2**63-1)}')
----> 3 np.int64(2**63) # overflow error
OverflowError: Python int too large to convert to C long
We can use the astype method to convert the data type:
A_int64 = A.astype(int) # converts to int64 by default
A_float32 = A.astype(np.float32) # converts to float32
for array in A_int64, A_float32:
print(array, array.dtype)
[[2 2]
[0 2]] int64
[[2. 2.]
[0. 2.]] float32
We have to be careful about assigning items of different types to an array.
A_int64[0,0] = 1
print(A_int64)
A_int64[0,0] = 0.5
print(A_int64) # intended assignment fails
np.array([int(1), float(1)]) # will be all floating point numbers
[[1 2]
[0 2]]
[[0 2]
[0 2]]
array([1., 1.])
Exercise Create a heterogeneous numpy array to store both integer and strings:
[0, 1, 2, 'a', 'b', 'c']
Hint: There is an numpy data type called object.
np.object?
### BEGIN SOLUTION
heterogeneous_np_array = np.array([*range(3),*'abc'],dtype=object)
### END SOLUTION
heterogeneous_np_array
array([0, 1, 2, 'a', 'b', 'c'], dtype=object)
Be careful when creating arrays of tuple/list:
for array in (np.array([(1,2),[3,4,5]],dtype=object),
np.array([(1,2),[3,4]],dtype=object)):
print(array, '\nshape:', array.shape, 'length:', len(array), 'size:', array.size)
[(1, 2) list([3, 4, 5])]
shape: (2,) length: 2 size: 2
[[1 2]
[3 4]]
shape: (2, 2) length: 2 size: 4
numpy provides many functions to create an array:
np.zeros?
np.zeros(0), np.zeros(1), np.zeros((2,3,4)) # Dimension can be higher than 2
(array([], dtype=float64),
array([0.]),
array([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]]))
np.ones?
np.ones(0, dtype=int), np.ones((2,3,4), dtype=int) # initialize values to int 1
(array([], dtype=int64),
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]]))
np.eye?
np.eye(0), np.eye(1), np.eye(2), np.eye(3) # identity matrices
(array([], shape=(0, 0), dtype=float64),
array([[1.]]),
array([[1., 0.],
[0., 1.]]),
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]]))
np.diag?
np.diag(range(1)), np.diag(range(2)), np.diag(np.ones(3),k=1) # diagonal matrices
(array([[0]]),
array([[0, 0],
[0, 1]]),
array([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 0.]]))
np.empty?
np.empty(0), np.empty((2,3,4), dtype=int) # create array faster without initialization
(array([], dtype=float64),
array([[[ 93838252494064, 0, 139638213065712,
139638235100976],
[139638213065776, 139638112650992, 139638112651056,
139638202180592],
[139638117153712, 139638117154288, 139638117154480,
139638117154032]],
[[139638186519088, 139638117153648, 139638112651120,
139638202049904],
[139638112651184, 139638233327216, 139638117164080,
139638202173520],
[139638117142240, 139638117154096, 139638112581168,
139638112580912]]]))
numpy also provides functions to build an array using rules.
np.arange?
np.arange(5), np.arange(4,5), np.arange(4.5,5.5,0.5) # like range but allow non-integer parameters
(array([0, 1, 2, 3, 4]), array([4]), array([4.5, 5. ]))
np.linspace?
np.linspace(4,5), np.linspace(4,5,11), np.linspace(4,5,11) # can specify number of points instead of step
(array([4. , 4.02040816, 4.04081633, 4.06122449, 4.08163265,
4.10204082, 4.12244898, 4.14285714, 4.16326531, 4.18367347,
4.20408163, 4.2244898 , 4.24489796, 4.26530612, 4.28571429,
4.30612245, 4.32653061, 4.34693878, 4.36734694, 4.3877551 ,
4.40816327, 4.42857143, 4.44897959, 4.46938776, 4.48979592,
4.51020408, 4.53061224, 4.55102041, 4.57142857, 4.59183673,
4.6122449 , 4.63265306, 4.65306122, 4.67346939, 4.69387755,
4.71428571, 4.73469388, 4.75510204, 4.7755102 , 4.79591837,
4.81632653, 4.83673469, 4.85714286, 4.87755102, 4.89795918,
4.91836735, 4.93877551, 4.95918367, 4.97959184, 5. ]),
array([4. , 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. ]),
array([4. , 4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. ]))
np.fromfunction?
np.fromfunction(lambda i, j: i * j, (3,4)) # can initialize using a function
array([[0., 0., 0., 0.],
[0., 1., 2., 3.],
[0., 2., 4., 6.]])
We can also reshape an array using the reshape method/function:
array = np.arange(2*3*4)
array.reshape?
(array,
array.reshape(2,3,4), # last axis index changes fastest
array.reshape(2,3,-1), # size of last axis calculated automatically
array.reshape((2,3,4), order='F')) # first axis index changes fastest
(array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23]),
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]),
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]),
array([[[ 0, 6, 12, 18],
[ 2, 8, 14, 20],
[ 4, 10, 16, 22]],
[[ 1, 7, 13, 19],
[ 3, 9, 15, 21],
[ 5, 11, 17, 23]]]))
flatten is a special case of reshaping an array to one dimension.
(Indeed, flatten returns a copy of the array but reshape returns a dynamic view whenever possible.)
array = np.arange(2*3*4).reshape(2,3,4)
array, array.flatten(), array.reshape(-1), array.flatten(order='F')
(array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]),
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23]),
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23]),
array([ 0, 12, 4, 16, 8, 20, 1, 13, 5, 17, 9, 21, 2, 14, 6, 18, 10,
22, 3, 15, 7, 19, 11, 23]))
Exercise Correct the following function to print every element of an array line-by-line.
def print_array_entries_line_by_line(array):
for i in array:
print(i)
def print_array_entries_line_by_line(array):
### BEGIN SOLUTION
for i in array.flatten():
print(i)
### END SOLUTION
print_array_entries_line_by_line(np.arange(2*3*4).reshape(2,3,4))
12.2.2. Operating on numpy arrays¶
How to verify the solution of a system of linear equations?
Before solving the system of linear equations, let us try to verify a solution to the equations:
numpy provides the function matmul and the operator @ for matrix multiplication.
print(np.matmul(A,np.array([0,0])) == b)
print(A @ np.array([0,0.5]) == b)
[False False]
[ True True]
Note that the comparison on numpy arrays returns a boolean array instead of a boolean value, unlike the comparison operations on lists.
To check whether all items are true, we use the all method.
print((np.matmul(A,np.array([0,0])) == b).all())
print((A @ np.array([0,0.5]) == b).all())
False
True
How to concatenate arrays?
We will operate on an augmented matrix of the coefficients:
numpy provides functions to create block matrices:
np.block?
C = np.block([A,b.reshape(-1,1)]) # reshape to ensure same ndim
C
array([[2., 2., 1.],
[0., 2., 1.]])
To stack an array along different axes:
array = np.arange(1*2*3).reshape(1,2,3)
for concat_array in [array,
np.hstack((array,array)), # stack along the first axis
np.vstack((array,array)), # second axis
np.concatenate((array,array), axis=-1), # last axis
np.stack((array,array), axis=0)]: # new axis
print(concat_array, '\nshape:', concat_array.shape)
[[[0 1 2]
[3 4 5]]]
shape: (1, 2, 3)
[[[0 1 2]
[3 4 5]
[0 1 2]
[3 4 5]]]
shape: (1, 4, 3)
[[[0 1 2]
[3 4 5]]
[[0 1 2]
[3 4 5]]]
shape: (2, 2, 3)
[[[0 1 2 0 1 2]
[3 4 5 3 4 5]]]
shape:
(1, 2, 6)
[[[[0 1 2]
[3 4 5]]]
[[[0 1 2]
[3 4 5]]]]
shape: (2, 1, 2, 3)
How to perform arithmetic operations on a numpy array?
To divide all the coefficients by \(2\), we can simply write:
D = C / 2
D
array([[1. , 1. , 0.5],
[0. , 1. , 0.5]])
Note that the above does not work for list.
C.tolist() / 2 # deep convert to list
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-30-7f30faff9f2c> in <module>
----> 1 C.tolist() / 2 # deep convert to list
TypeError: unsupported operand type(s) for /: 'list' and 'int'
Arithmetic operations on numpy arrays apply if the arrays have compatible dimensions. Two dimensions are compatible when
they are equal, except for
components equal to 1.
numpy uses broadcasting rules to stretch the axis of size 1 up to match the corresponding axis in other arrays.
C / 2 is a example where the second operand \(2\) is broadcasted to a \(2\)-by-\(2\) matrix before the elementwise division. Another example is as follows.
three_by_one = np.arange(3).reshape(3,1)
one_by_four = np.arange(4).reshape(1,4)
print(f'''
{three_by_one}
*
{one_by_four}
==
{three_by_one * one_by_four}
''')
[[0]
[1]
[2]]
*
[[0 1 2 3]]
==
[[0 0 0 0]
[0 1 2 3]
[0 2 4 6]]
Next, to subtract the second row of the coefficients from the first row:
D[0,:] = D[0,:] - D[1,:]
D
array([[1. , 0. , 0. ],
[0. , 1. , 0.5]])
Notice the use of commas to index different dimensions instead of using multiple brackets:
assert (D[0][:] == D[0,:]).all()
Using this indexing technique, it is easy extract the last column as the solution to the system of linear equations:
x = D[:,-1]
x
array([0. , 0.5])
This gives the desired solution \(x_0=0\) and \(x_1=0.5\) for
numpy provides many convenient ways to index an array.
B = np.arange(2*3).reshape(2,3)
B, B[(0,1),(2,0)] # selecting the corners using integer array
(array([[0, 1, 2],
[3, 4, 5]]),
array([2, 3]))
B = np.arange(2*3*4).reshape(2,3,4)
B, B[0], B[0,(1,2)], B[0,(1,2),(2,3)], B[:,(1,2),(2,3)] # pay attention to the last two cases
(array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]),
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]),
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]),
array([ 6, 11]),
array([[ 6, 11],
[18, 23]]))
assert (B[...,-1] == B[:,:,-1]).all()
B[...,-1] # ... expands to selecting all elements of all previous dimensions
array([[ 3, 7, 11],
[15, 19, 23]])
B[B>5] # indexing using boolean array
array([ 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22,
23])
Finally, the following function solves a system of 2 linear equations with 2 variables.
def solve_2_by_2_system(A,b):
'''Returns the unique solution of the linear system, if exists,
else returns None.'''
C = np.hstack((A,b.reshape(-1,1)))
if C[0,0] == 0: C = C[(1,0),:]
if C[0,0] == 0: return None
C[0,:] = C[0,:] / C[0,0]
C[1,:] = C[1,:] - C[0,:] * C[1,0]
if C[1,1] == 0: return None
C[1,:] = C[1,:] / C[1,1]
C[0,:] = C[0,:] - C[1,:] * C[0,1]
return C[:,-1]
# tests
for A in (np.eye(2),
np.ones((2,2)),
np.stack((np.ones(2),np.zeros(2))),
np.stack((np.ones(2),np.zeros(2)),axis=1)):
print(f'A={A}\nb={b}\nx={solve_2_by_2_system(A,b)}\n')
A=[[1. 0.]
[0. 1.]]
b=[1. 1.]
x=[1. 1.]
A=[[1. 1.]
[1. 1.]]
b=[1. 1.]
x=None
A=[[1. 1.]
[0. 0.]]
b=[1. 1.]
x=None
A=[[1. 0.]
[1. 0.]]
b=[1. 1.]
x=None
12.2.3. Universal functions¶
Why does the first line of code below return two arrays but the second code return only one array? Shouldn’t the first line of code return the following?
array([[(0,1), (0,2), (0,3)],
[(1,1), (1,2), (1,3)]])
print(np.fromfunction(lambda i,j:(i,j), (2,3), dtype=int))
print(np.fromfunction(lambda i,j:(i*j), (2,3), dtype=int))
(array([[0, 0, 0],
[1, 1, 1]]), array([[0, 1, 2],
[0, 1, 2]]))
[[0 0 0]
[0 1 2]]
From the documentation, fromfunction applies the given function to the two arrays as arguments.
The first line of code returns a tuple of the arrays.
The second line of code multiplies the two arrays to give one array, according to how multiplication works for numpy arrays.
Indeed, numpy implements universal/vectorized functions/operators that take arrays as arguments and perform operations with appropriate broadcasting rules. The following is an example that uses the universal function np.sin:
import matplotlib.pyplot as plt
@widgets.interact(a=(0,5,1),b=(-1,1,0.1))
def plot_sin(a=1,b=0):
x = np.linspace(0,2*math.pi)
plt.plot(x,np.sin(a*x+b*math.pi)) # np.sin, *, + are universal functions
plt.title(r'$\sin(ax+b\pi)$')
plt.xlabel(r'$x$ (radian)')
In addition to making the code shorter, universal functions are both efficient and flexible. (Recall the Monte Carlo simulation to approximate \(\pi\).)
Exercise Explain how the Monte Carlo simulation work using universal functions:
def np_approximate_pi(n):
in_circle = (np.random.random((n,2))**2).sum(axis=-1) < 1
mean = 4 * in_circle.mean()
std = 4 * in_circle.std() / n**0.5
return np.array([mean - 2*std, mean + 2*std])
random.randomgenerates a numpy array for \(n\) points in the unit square randomly.sumsums up the element along the last axis to give the squared distance.<returns the boolean array indicating whether each point is in the first quadrant of the inscribed circle.meanandstdreturns the mean and standard deviation of the boolean array with True and False interpreted as 1 and 0 respectively.