Abstract¶
An important engineering application of computer science is numerical analysis. This lecture introduces estimation using Monte Carlo simulations and basic linear algebra for solving multiple linear equations. Readers will learn to use NumPy arrays instead of lists to implement numerical analysis efficiently, incorporating the concepts of universal functions and broadcasting.
from __init__ import install_dependencies
await install_dependencies()Monte Carlo simulation¶
What is Monte Carlo simulation?
It is a statistical method named after a Casino in Monaco:
I suggested an obvious name for the statistical method — a suggestion not unrelated to the fact that Stan had an uncle who would borrow money from relatives because he “just had to go to Monte Carlo.”
(N. Metropolis, “The Beginning of the Monte Carlo Method.”)
It would be nice to simulate the casino so Ulam’s uncle did not need to borrow money to play in the casino.
Actually...,
- Monte Carlo is the code name of the secret project for creating the hydrogen bomb.
- Nicholas Metropolis and Stan Ulam worked with John von Neumann to program the first electronic computer ENIAC to simulate a computational model of a thermonuclear reaction.
As a simple illustration, we will compute the value of π:
math.piInstead of using pi from math, can we compute π directly? Consider a seemingly unrelated math problem:
What is the chance a random point in a square lies in the inscribed circle?

Uniformly random points in a square. Green (Red) points are inside (outside) the inscribed circle. (source code)
By relating the chance of a random event to the quantity we want to compute, we can compute the quantity by simulating the random event. This method is called the Monte Carlo simulation:
def approximate_pi(n):
### BEGIN SOLUTION
return (
4
* len(
[True for i in range(n) if random.random() ** 2 + random.random() ** 2 < 1]
)
/ n
)
### END SOLUTION%%timeit -n 1 -r 1
print(f"Approximate: {approximate_pi(10**7)}\nGround truth: {math.pi}")How accurate is the approximation?
The following uses a powerful library NumPy to return a -confidence interval.
def np_approximate_pi(n):
in_circle = (np.random.random((n, 2)) ** 2).sum(axis=-1) < 1
mean = 4 * in_circle.mean()
std = 4 * in_circle.std() / n ** 0.5
return np.array([mean - 2 * std, mean + 2 * std])%%timeit -n 1 -r 1
interval = np_approximate_pi(10**7)
print(
f"""95%-confidence interval: {interval}
Estimate: {interval.mean():.4f} ± {(interval[1]-interval[0])/2:.4f}
Ground truth: {math.pi}"""
)Is Numpy faster?
The computation done using NumPy is over 5 times faster despite the additional computation of the standard deviation.
We can increase further to obtain a more accurate solution:
interval = np_approximate_pi(10**8)
print(
f"""95%-confidence interval: {interval}
Estimate: {interval.mean():.4f} ± {(interval[1]-interval[0])/2:.4f}
Ground truth: {math.pi}"""
)There are faster methods to approximate π, such as the BBP Formula and Chudnovsky algorithm, but the Monte-Carlo method is helpful in complicated situations.
%%ai chatgpt -f text
Write a python program `print_pi(n)` to print pi to `n` decimal places.
Avoid the precision limit of float.%%ai chatgpt -f text
Provide an example of an application where Monte Carlo simulation is the only feasible computational method and no superior alternatives are known.%%ai chatgpt -f text
Explain how the accuracy of the estimates by Monte Carlo simulation can be improved by importance sampling?Linear Algebra¶
How to solve a linear equation?
Given the following linear equation in variable with real-valued coefficient and ,
what is the value of that satisfies the equation?
Complete the following function to return either the unique solution of or None if a unique solution does not exist.
def solve_linear_equation(a, b):
### BEGIN SOLUTION
return b / a if a != 0 else None
### END SOLUTION
@widgets.interact(a=(0, 5, 1), b=(0, 5, 1))
def linear_equation_solver(a=2, b=3):
print(
f"""linear equation: {a}x = {b}
solution: x = {solve_linear_equation(a,b)}"""
)How to solve multiple linear equations?
In the general case, we have a system of linear equations and variables:
where
- for are the variables, and
- and for and are the coefficients.
A fundamental problem in linear algebra is to compute the unique solution to the system if it exists.
We will consider the simpler 2-by-2 system with 2 variables and 2 equations:
To get an idea of the solution, suppose
The system of equations becomes
which gives the solution directly.
What about instead?
To obtain the solution, we divide both equations by 2:
What if instead?
The second equation gives the solution of , and we can use the solution in the first equation to solve for . More precisely:
- Subtract the second equation from the first one:
- Divide both equations by 2:
The above operations are called row operations in linear algebra: Each row is an equation.
A system of linear equations can be solved by the linear operations of
- multiplying an equation by a constant, and
- subtracting one equation from another.
How to write a program to solve a general 2-by-2 system? We will use the NumPy library.
Creating NumPy arrays¶
How to store the coefficients?
In linear algebra, a system of equations such as
is written concisely in matrix form as :
where is the matrix multiplication
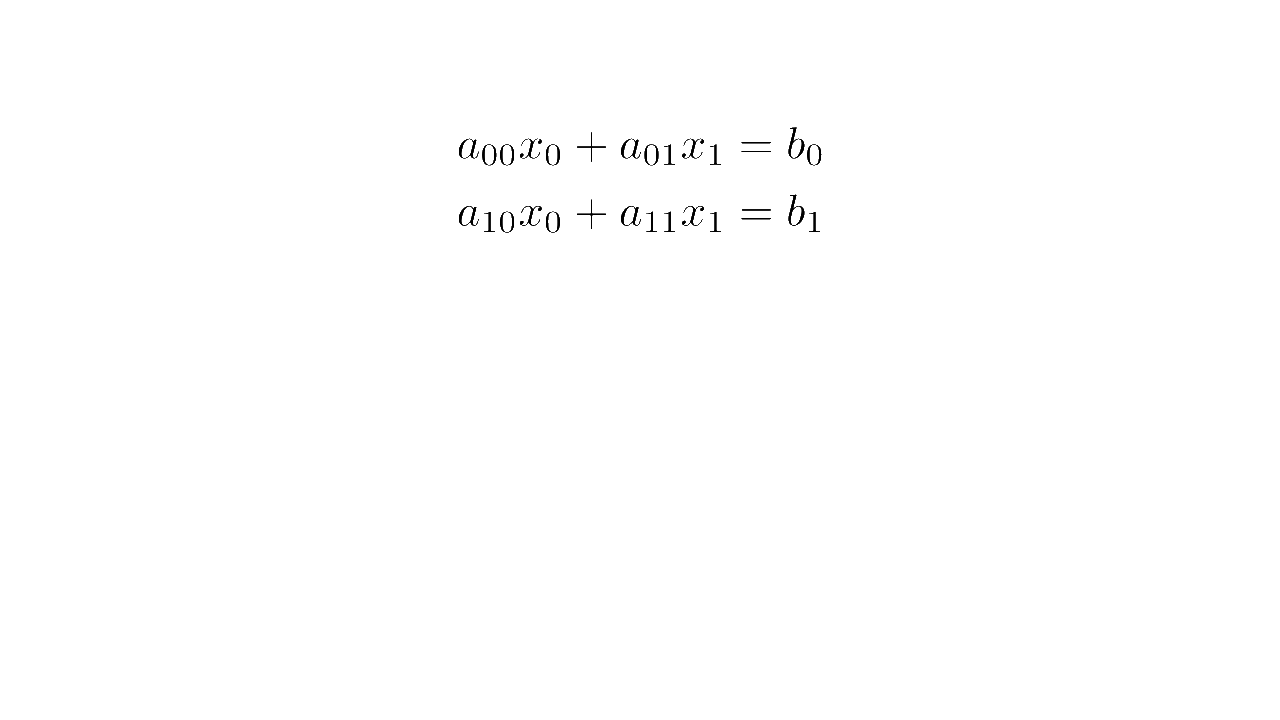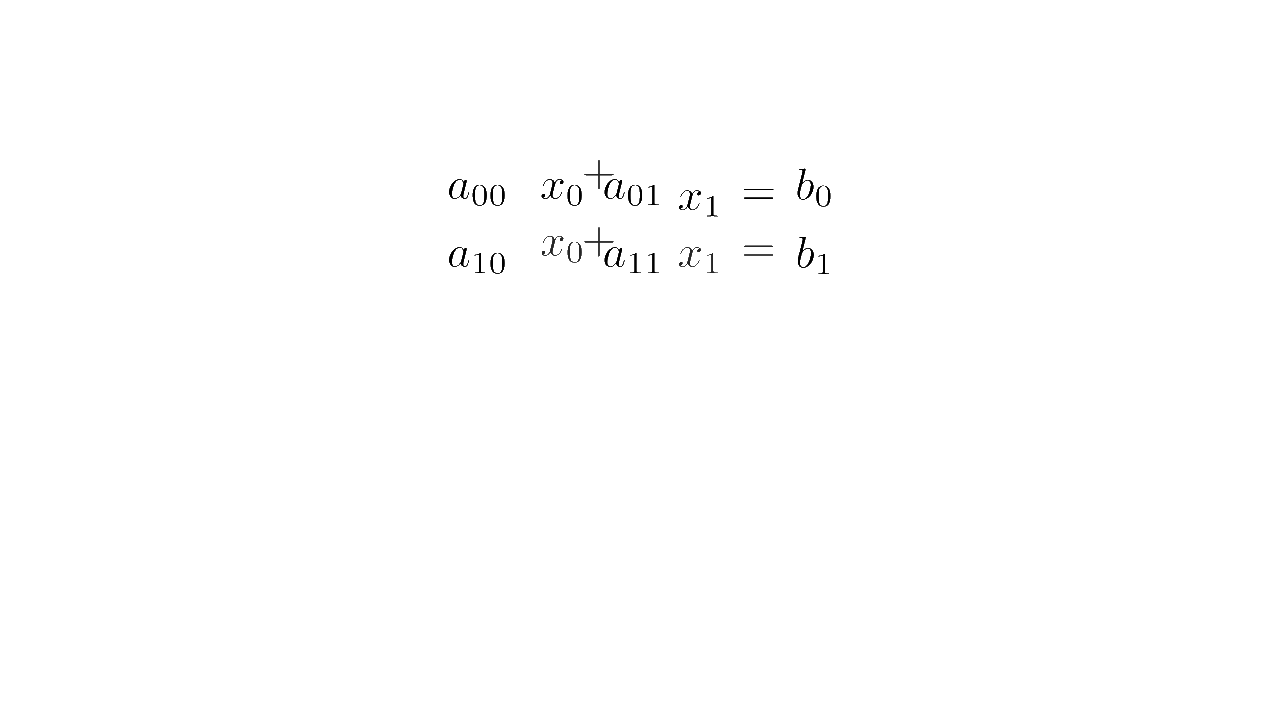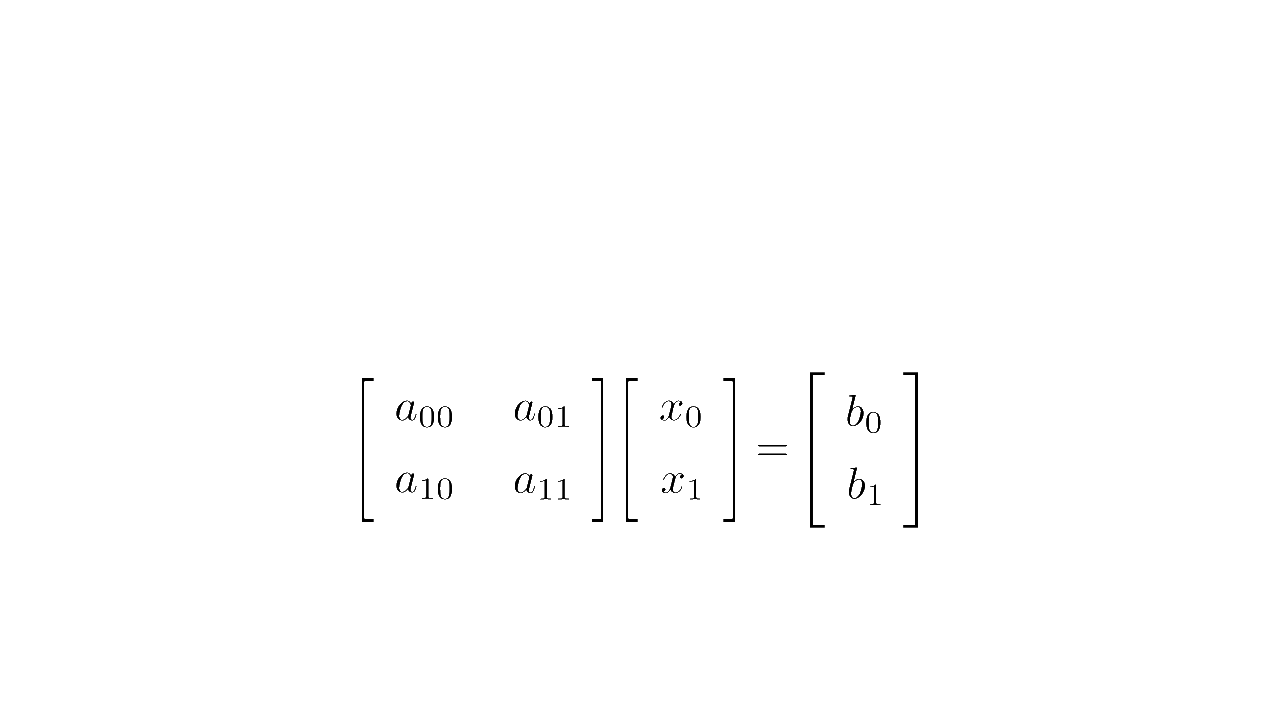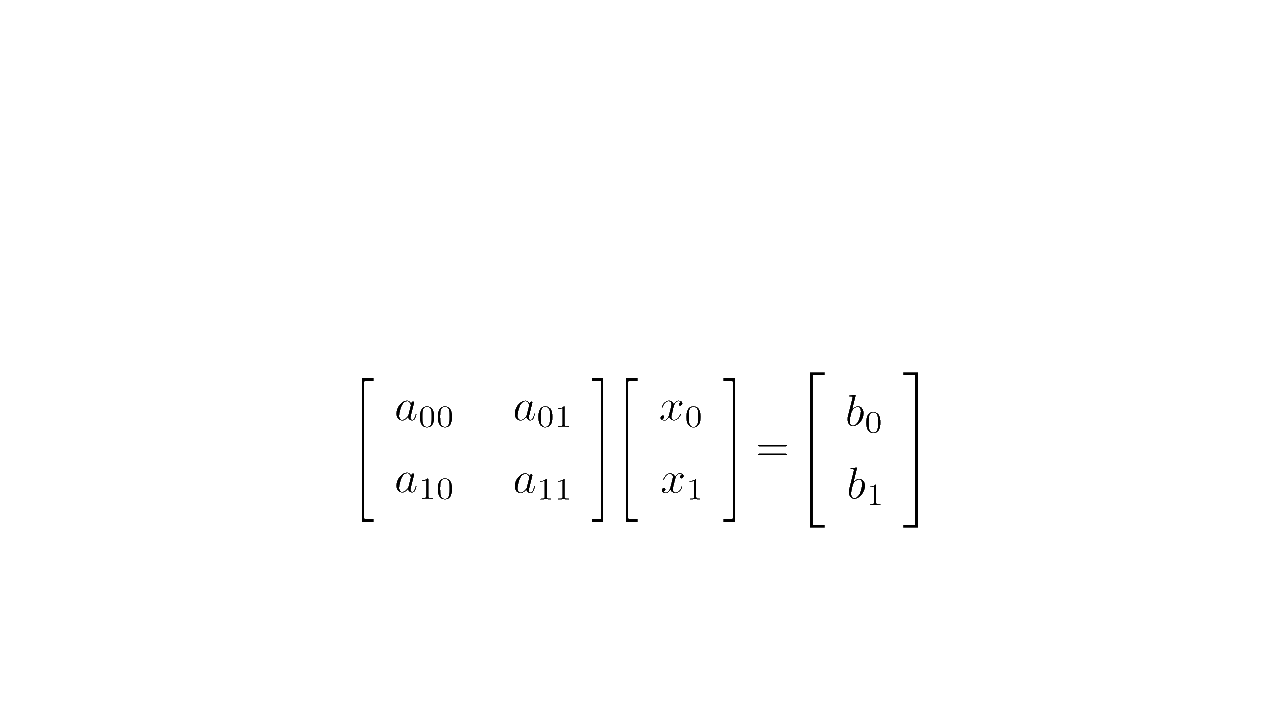
Matrix form (source code)
We say that is a matrix and its dimension/shape is 2-by-2:
- The first dimension/axis has size 2. We also say that the matrix has 2 rows.
- The second dimension/axis has size 2. We also say that the matrix has 2 columns. and are called column vectors, which are matrices with one column.
Instead of using list to store the matrix, we will use a NumPy array.
A = np.array([[2.0, 2], [0, 2]])
b = np.array([1.0, 1])
A, bCompared to list, NumPy array is often more efficient and has more attributes.
array_attributes = set(attr for attr in dir(np.array([])) if attr[0] != "_")
list_attributes = set(attr for attr in dir(list) if attr[0] != "_")
print("\nCommon attributes:\n", *(array_attributes & list_attributes))
print("\nArray-specific attributes:\n", *(array_attributes - list_attributes))
print("\nList-specific attributes:\n", *(list_attributes - array_attributes))The following attributes give the dimension/shape, number of dimensions, size, and data type.
for array in A, b:
print(
f"""{array}
shape: {array.shape}
ndim: {array.ndim}
size: {array.size}
dtype: {array.dtype}
"""
)Note that the function len only returns the size of the first dimension:
assert A.shape[0] == len(A)
len(A)Unlike list, every NumPy array has a data type. For efficient computation/storage, numpy implements different data types with different storage sizes:
np.byte, np.short, np.intc
np.ubyte, np.ushort, np.uintc, np.uint
np.half, np.single, np.double, np.longfloat
np.csingle, np.cdouble, np.clongdoubleE.g., int64 is the 64-bit integer. Unlike int, int64 has a range.
%%optlite -h 400
import numpy as np
min_int64 = np.int64(-2**63)
max_int64 = np.int64(2**63-1)
np.int64(2 ** 63) # overflow errorWe can use the astype method to convert the data type:
A_int64 = A.astype(int) # converts to int64 by default
A_float32 = A.astype(np.float32) # converts to float32
for array in A_int64, A_float32:
print(array, array.dtype)We must be careful about assigning items of different types to an array.
A_int64[0, 0] = 1
print(A_int64)
A_int64[0, 0] = 0.5
print(A_int64) # intended assignment fails
np.array([int(1), float(1)]) # will be all floating point numbersCreate a heterogeneous NumPy array to store both integers and strings:
[0, 1, 2, 'a', 'b', 'c']Hint
Use the object type.
### BEGIN SOLUTION
heterogeneous_np_array = np.array([*range(3), *"abc"], dtype=object)
### END SOLUTION
heterogeneous_np_arrayBe careful when creating arrays of tuple/list:
%%optlite -h 350
import numpy as np
a1 = np.array([(1, 2), [3, 4, 5]], dtype=object)
print(a1.shape, a1.size)
a2 = np.array([(1, 2), [3, 4]], dtype=object)
print(a2.shape, a2.size)NumPy provides many functions to create an array:
%%optlite -h 400 -l
import numpy as np
a = [np.zeros(0)]
a.append(np.zeros(1, dtype=int))
a.append(np.zeros((2, 3, 4)))%%optlite -h 400 -l
import numpy as np
a = [np.empty(2)]
a.append(np.empty((2, 3, 4),
dtype=int))%%optlite -h 400 -l
import numpy as np
a = [np.ones(2)]
a.append(np.ones((2, 3, 4),
dtype=int))%%optlite -l -h 400
import numpy as np
a = [np.eye(2)]
a.append(np.eye(3, dtype=int))%%optlite -l -h 400
import numpy as np
a = [np.diag(range(1))]
a.append(np.diag(range(2)))
a.append(np.diag(np.ones(3), k=1))
# 1 above main diagonalNumPy also provides functions to build an array using rules.
%%optlite -l -h 400
import numpy as np
a = [np.arange(5)]
# like range but allow non-integer parameters
a.append(np.arange(2.5, 5, 0.5))%%optlite -l -h 400
import numpy as np
# can specify the number of points instead of the step size
a = [np.linspace(0, 4, 5)]
a.append(np.linspace(2.5, 4.5, 5))%%optlite -l -h 400
import numpy as np
a = np.fromfunction(lambda i, j: i * j, (3, 4))We can also reshape an array using the reshape method/function:
%%optlite -l -h 500
import numpy as np
a = np.arange(2 * 3 * 4)
c1 = a.reshape(2, 3, 4)
# automatically calculate the size specified as `-1`
c2 = a.reshape(2, 3, -1)%%optlite -l -h 500
import numpy as np
a = np.arange(2 * 3 * 4)
# default C ordering
c = a.reshape((2, 3, -1), order="C")
# F ordering
f = a.reshape((2, 3, -1), order="F")The C ordering and F ordering can be implemented using list comprehension:
%%optlite -l -h 500
import numpy as np
a = np.arange(2 * 3 * 4)
# last axis index changes fastest
c = np.array(
[[[a[i*3*4+j*4+k]
for k in range(4)]
for j in range(3)]
for i in range(2)])
# first axis index changes fastest
f = np.array(
[[[a[i+j*2+k*3*2]
for k in range(4)]
for j in range(3)]
for i in range(2)])When restricted to 2-dimension:
- C-style (row-major) order is like English writing, where one writes row by row.
- F-style (column-major) order is like traditional Chinese writing, where one writes column by column.
ravel is a particular case of reshaping an array to one dimension.
A similar function flatten returns a copy of the array but ravel and reshape returns a dynamic view whenever possible.
array = np.arange(2 * 3 * 4).reshape(2, 3, 4)
array, array.ravel(), array.reshape(-1), array.ravel(order="F")Correct the following function to print every element of an array line-by-line.
def print_array_entries_line_by_line(array):
for i in array:
print(i)def print_array_entries_line_by_line(array):
### BEGIN SOLUTION
for i in array.flatten():
print(i)
### END SOLUTION
print_array_entries_line_by_line(np.arange(2 * 3 * 4).reshape(2, 3, 4))Operating on arrays¶
How to verify the solution of a system of linear equations?
Before solving the system of linear equations, let us try to verify a solution to the equations:
NumPy provides the function matmul and the operator @ for matrix multiplication.
print(np.matmul(A, np.array([0, 0])) == b)
print(A @ np.array([0, 0.5]) == b)Note that the comparison on NumPy arrays returns a boolean array instead of a boolean value, unlike the comparison operations on lists.
To check whether all items are true, we use the all method.
print((np.matmul(A, np.array([0, 0])) == b).all())
print((A @ np.array([0, 0.5]) == b).all())How to concatenate arrays?
We will operate on an augmented matrix of the coefficients:
NumPy provides functions to create block matrices:
np.block?
C = np.block([A, b.reshape(-1, 1)]) # reshape to ensure same ndim
CTo stack an array along different axes:
array = np.arange(1 * 2 * 3).reshape(1, 2, 3)
for concat_array in [
array,
np.hstack((array, array)), # stack along the second axis with index 0
np.vstack((array, array)), # stack along the first axis with index 1
np.concatenate((array, array), axis=-1), # last axis
np.stack((array, array), axis=0),
]: # new axis
print(concat_array, "\nshape:", concat_array.shape)How to perform arithmetic operations on a NumPy array?
To divide all the coefficients by 2, we can write:
D = C / 2
DNote that the above does not work for list.
%%optlite -l -h 500
[[2, 2, 1], [0, 2, 1]] / 2Arithmetic operations on NumPy arrays apply if the arrays have compatible dimensions. Two dimensions are compatible when
- they are equal, except for
- components equal to 1.
NumPy uses broadcasting rules to stretch the axis of size 1 up to match the corresponding axis in other arrays. C / 2 is an example where the second operand 2 is broadcasted to a 2-by-2 matrix before the elementwise division. Another example is as follows.
three_by_one = np.arange(3).reshape(3, 1)
one_by_four = np.arange(4).reshape(1, 4)
print(
f"""
{three_by_one}
*
{one_by_four}
==
{three_by_one * one_by_four}
"""
)%%ai chatgpt -f text
Explain the broadcasting rule intuitively in one paragraph using an analogy.Next, to subtract the second row of the coefficients from the first row:
D[0, :] = D[0, :] - D[1, :]
DNotice the use of commas to index different dimensions instead of using multiple brackets:
assert (D[0][:] == D[0, :]).all()Using this indexing technique, it is easy to extract the last column as the solution to the system of linear equations:
x = D[:, -1]
xThis gives the desired solution and for
NumPy provides many convenient ways to index an array.
B = np.arange(2 * 3).reshape(2, 3)
B, B[(0, 1), (2, 0)] # selecting the corners using integer arrayB = np.arange(2 * 3 * 4).reshape(2, 3, 4)
B, B[0], B[0, (1, 2)], B[0, (1, 2), (2, 3)], B[
:, (1, 2), (2, 3)
] # pay attention to the last two casesassert (B[..., -1] == B[:, :, -1]).all()
B[..., -1] # ... expands to selecting all elements of all previous dimensionsB[B > 5] # indexing using boolean arrayFinally, the following function solves 2 linear equations with 2 variables.
def solve_2_by_2_system(A, b):
"""Returns the unique solution of the linear system, if exists,
else returns None."""
C = np.hstack((A, b.reshape(-1, 1)))
if C[0, 0] == 0:
C = C[(1, 0), :]
if C[0, 0] == 0:
return None
C[0, :] = C[0, :] / C[0, 0]
C[1, :] = C[1, :] - C[0, :] * C[1, 0]
if C[1, 1] == 0:
return None
C[1, :] = C[1, :] / C[1, 1]
C[0, :] = C[0, :] - C[1, :] * C[0, 1]
return C[:, -1]# tests
for A in (
np.eye(2),
np.ones((2, 2)),
np.stack((np.ones(2), np.zeros(2))),
np.stack((np.ones(2), np.zeros(2)), axis=1),
):
print(f"A={A}\nb={b}\nx={solve_2_by_2_system(A,b)}\n")Universal functions¶
NumPy implements universal/vectorized functions/operators that take arrays as arguments and perform operations with appropriate broadcasting rules. The following is an example that uses the universal function np.sin:
@widgets.interact(a=(0, 5, 1), b=(-1, 1, 0.1))
def plot_sin(a=1, b=0):
plt.figure(1, clear=True)
plt.title(r"$\sin(ax+b\pi)$")
plt.xlabel(r"$x$ (radian)")
x = np.linspace(0, 2 * math.pi)
plt.plot(x, np.sin(a * x + b * math.pi)) # np.sin, *, + are universal functions
plt.show()In addition to making the code shorter, universal functions are both efficient and flexible. Recall the Monte Carlo simulation to approximate π:
Explain the universal functions used in the following Monte Carlo simulation:
def np_approximate_pi(n):
in_circle = (np.random.random((n,2))**2).sum(axis=-1) < 1
mean = 4 * in_circle.mean()
std = 4 * in_circle.std() / n**0.5
return np.array([mean - 2*std, mean + 2*std])Solution to Exercise 5
random.randomgenerates a numpy array for points in the unit square randomly.sumsums up the element along the last axis to give the squared distance.<returns the boolean array indicating whether each point is in the first quadrant of the inscribed circle.meanandstdreturns the mean and standard deviation of the boolean array with True and False interpreted as 1 and 0, respectively.
%%ai chatgpt -f text
Explain in a paragraph why universal functions in numpy are far more efficient
than applying a function to each element of a list individually.- Metropolis, N., & Ulam, S. (1949). The Monte Carlo Method. Journal of the American Statistical Association, 44(247), 335–341. 10.1080/01621459.1949.10483310